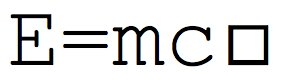지난 번 “대학수학 맛보기”에서 적분 이야기를 했으니, 다음은 미분 이야기를 하면 적당할 것 같다. 뭔가 순서가 바뀐 것 같은 느낌이 든다면, 기분 탓이다. 고등학교에서 미분을 처음 배울 때, 함수 \(y=f(x)\)의 미분을 다음과 같이 정의한다.
\[\frac{dy}{dx} = \lim_{\Delta x \to 0} \frac{\Delta y}{\Delta x} = \lim_{\Delta x \to 0} \frac{f(x+\Delta x)-f(x)}{\Delta x}\]
그러고 \(dy/dx\)를 “미분계수(differential coefficient)”라고 부른다. 생각해 보면 참으로 기묘하고 마술 같은 식이다. 이름부터 이상하다. 저 값이 어딜 봐서 “계수”라는 말인가? 또, 순진하게(?) 생각하면 \(dx=\lim_{\Delta x \to 0}\Delta x\)처럼 보이는데, 그러면 분모가 \(0\)이 되어 버린다. 그러니까, \(dx\)는 \(\Delta x\)에 해당하는 값이면서 \(0\)은 아니어야 하는 이상한 일이 벌어진다. 아니, 애초에 \(dx\)니 \(dy\)니 하는 게 무엇인지부터 분명하지 않다. 수를 나타낸다고 하면 분모와 분자가 모두 \(0\)인 분수가 되어 말이 안 되고, 수가 아니라고 하면 \(dy\)를 \(dx\)로 나눈다는 게 말이 안 된다.
실제로 뉴턴과 라이프니츠가 미적분학을 개발했을 때 직면한 문제점이 바로 이것이었다. \(dx\)와 \(dy\)는 수도 아니고, 수가 아닌 것도 아닌 정체불명의 그 무엇이었다.
라이프니츠는 \(dx\)와 \(dy\)를 “미분(differential)”이라 부르고 무한소(infinitesimal)로 생각하였다. \(dy\)를 \(dx\)로 나누는 대신
\[dy=(?)dx\]
꼴로 생각하고 물음표에 해당하는 값을 “미분에 붙어있는 수”라는 뜻에서 “미분계수”라고 불렀다. 미분계수가 미분계수로 불리는 이유이다.
아마도 무한소를 생각하는 과정에서 라이프니츠 철학의 핵심 개념인 모나드(monad)를 착안하지 않았을까 싶은데, 무한소를 이용한 설명은 그럴 듯하기는 하지만, 무한소라는 개념 자체가 모호하여 논리적으로는 한계가 있었다. 라이프니츠는 “연산 규칙을 분명하게 정해 놓고 이 규칙들을 적절히 적용하기만 한다면, 그 개념이 다소 모호하다고 해도 합리적이고 올바른 결과를 얻게 된다.”라고 하였다. 어찌 보면 철학자답지 않은 발언 같기도 한데, 어쨌든 그의 통찰력만은 대단했다.
미분 개념의 모호함 때문에, 현행 고등학교 교육과정에서는 미분계수 \(dy/dx\)를 분수처럼 생각하지 않고, \(d/dx\)를 하나의 기호로 다루도록 하고 있다. 이런 이유로, 분수가 아니라는 뜻에서, \(dy/dx\)를 “디 와이 디 엑스”로 읽어야만 한다고 가르치는 경우도 있는데, 그건 좀 심한 것 같다. 어찌 됐든 저 모양은 분수꼴이므로 “디 엑스 분의 디 와이”라고 읽어서 안 될 이유는 없다. 무엇보다도 라이프니츠가 애초에 분수 모양을 의도하고 만든 기호이므로, 분수처럼 생긴 것을 분수처럼 부르지 못하면 억울하지 않은가. 홍길동도 아닌데.
라이프니츠의 착상(의 위력)을 가장 잘 보여주는 것은 아마도 다음 등식
\[\frac{dz}{dx} = \frac{dz}{dy}\times\frac{dy}{dx}\]
일 것 같다. 바로 연쇄 법칙(chain rule)이다. 모양만 놓고 보면 \(dy\)를 약분하면 등식이 성립한다. 실제로 이 증명도 \(dy\)를 약분하는 것과 별로 다르지 않다. 다만 \(dy\)가 \(0\)이 되는 경우, 즉 함수 \(y(x)\)의 증가량이 \(0\)인 경우를 따로 다루는 것이 조금 다를 뿐이다.
고등학교에서 \(dx\)와 \(dy\)를 분리해서 생각하지 않도록 한다지만, 사실 적분만 봐도 이런 원칙은 바로 이상해진다. 적분
\[\int f(x)\,dx\]
는 \(dx\)를 분리해서 표기하고 있으며, \(x=g(t)\)로 치환적분할 때
\[\int f(x)\,dx = \int f(g(t)) \frac{dx}{dt}\,dt\]
는 분모의 \(dt\)와 마지막 \(dt\)가 약분되는 형태를 드러내는 식이고, 무엇보다 저런 치환적분을 할 때 \(x=g(t)\)의 양변을 \(t\)로 미분한다면서
\[dx = g'(t)\,dt\]
라는 계산을 겁도 없이(?) 마구 한다는 점에서 \(dx\)니 \(dy\)니 하는 것을 분리해서 생각하고 있다. 정확히 말하면, 분리해서 생각해도 문제가 잘 풀리도록 기호가 설계되어 있다.
이런 엉성한(?) 개념으로 뉴턴, 라이프니츠는 물론, 오일러, 가우스, 코시 등등 수많은 천재 수학자들이 어마어마한 업적을 쌓아올렸다. 그러다 이 개념을 더 정교하게 다듬고 확장하는 과정에서 해석학이라는 분야로 크게 발전하였다. 어떤 면에서는, 미적분학은 좋은 함수가 가지고 있는 좋은 성질을 공부하는 과목이고, 해석학은 나쁜 함수가 가지고 있는 나쁜 성질을 공부하는 과목이라 할 수 있을지도.
고등학교에서 배우는 17세기 수학과는 달리 현대 수학에서는 벡터 개념을 이용하여 \(dx\)와 \(dy\)를 수학적으로 엄밀하게 잘 다룰 수 있다.
함수 \(y=f(x)\)의 그래프를 그렸다고 생각하자. 지금은 좋은 함수의 좋은 성질을 설명하는 것이므로, 이 함수는 미분 가능한 함수로 생각한다. 미분을 한다는 것은 함수에 대한 선형 근사를 찾는 것이라 할 수 있고, 함수의 그래프를 생각하면 각 점에서 접선을 구하는 것이라 할 수 있다. 접점은 주어져 있으므로, 접선의 기울기만 알면 접선을 그릴 수 있다.
이제 접점 \(\mathrm{P}\)를 시점으로 하고 접선의 한 점을 종점으로 하는 벡터를 그리면, 접벡터들의 집합 \(T_{\mathrm{P}}\)는 1차원 벡터 공간이 된다. 이 벡터 공간에서 벡터를 하나 골라 \(\mathbf{v}\)라 하자. 이때 \(dx\)와 \(dy\)는 \(\mathbf{v}\)에 실수를 대응시키는 함수로 생각한다. \(dx(\mathbf{v})\)는 \(x\)축 방향 변화량, \(dy(\mathbf{v})\)는 \(y\)축 방향 변화량을 뜻한다. 아래 그림에서 \(a=dx(\mathbf{v})\)이고 \(b=dy(\mathbf{v})\)이다.

벡터 \(\mathbf{v}\)가 접선에 놓여 있으므로, 두 실수 \(dx(\mathbf{v})\)와 \(dy(\mathbf{v})\)는 일정한 비를 이룬다. 즉,
\[dy(\mathbf{v}) = k \, dx(\mathbf{v})\]
가 되고, 접선의 기울기인 비례상수 \(k\)는 \(\mathbf{v}\)의 크기가 아무리 작아도 일정하다. 이 부분이 바로 무한소를 벡터 개념으로 대체한 것이다. 임의의 \(\mathbf{v}\)에 대하여 위의 등식이 성립하므로, 간단히
\[dy = k\,dx\]
라 둘 수 있다. 그러니까 위 등식은 두 함수 \(dx:T_{\mathrm{P}} \to \mathbb{R}\)와 \(dy:T_{\mathrm{P}} \to \mathbb{R}\)가 비례 관계임을 뜻한다. \(k\)의 값은 접점 \(\mathrm{P}\)의 좌표(의 \(x\)-성분)에 따라 결정되므로, \(x\)에 대한 함수로 생각할 수 있다. 원래 함수 \(y=f(x)\)로부터 유도되어 나오는 이 새로운 함수를 도함수(導函數, derivative)라 하고 \(f'(x)\)로 나타내면,
\[dy=f'(x)\,dx\]
라는 익숙한 등식이 된다. \(dx\)와 \(dy\)가 무엇인지, 분리해서 써도 되는지 고민할 필요가 없다!
함수 \(dx\)처럼 벡터에 실수를 대응시키는 함수를 특별히 미분형식(differential form)이라 부른다. 이제 같은 방식으로 생각하면, 적분이란 미분형식에 작용하는 연산자로 생각할 수 있다. 그러니까, 이런 관점에서는, 적분 \(\int_a^b f(x)\,dx\)에서 기호 \(\int_a^b\)가 적용되는 대상은 함수 \(f(x)\)가 아니라 미분형식 \(f(x)\,dx\)이고, 적분은 [벡터에 실수를 대응시키는 미분형식]에 [실수]를 대응시키는 특별한 연산자가 된다.
사실 이런 개념 없이도 미분계수를 정의하고, 주어진 함수를 미분하고 적분하는 것은 얼마든지 할 수 있다. 실제로 고등학교 수학 교과서에서 그렇게 하고 있으니까. 그럼에도 이런 복잡해 보이는 고생을 사서 하는 이유는, 이와 같이 한 개념을 엄밀하게 정의하면 그 개념을 확장하는 것이 매우 논리적이고 자연스러워지기 때문이다.
예를 들어, 2변수 함수 \(z=f(x,y)\)에서 “미분”을 어떻게 정의할 수 있을까? 이 경우는 변수가 두 개이므로, \(dz/dx\)나 \(dz/dy\) 하나만으로는 함수를 묘사하기가 어렵다. 이제 앞서 보았던 미분형식을 생각하면, 우리가 해야할 일은 \(dz(\mathbf{v})\)를 \(dx(\mathbf{v})\)와 \(dy(\mathbf{v})\)에 대한 식으로 나타내는 것임을 알 수 있다. 여기서 벡터 \(\mathbf{v}\)는 당연히 \(z=f(x,y)\)로 주어지는 곡면의 접평면에 속하는 벡터가 된다. 1변수 함수에서 접선에 속하는 접벡터를 생각했던 것처럼, 2변수 함수에서는 접평면에 속하는 접벡터를 생각하는 것이다.
벡터 \(\mathbf{v}\)가 점 \(\mathrm{P}\)에서 접하는 평면 위에 놓여 있다고 하면, 세 축 방향의 증가량들 사이의 관계식은
\[dz(\mathbf{v}) = (♠︎)\,dx(\mathbf{v}) + (♡)\,dy(\mathbf{v})\]
라는 일차식 형태로 표현되고, \(dy(\mathbf{v})=0\)인 벡터 \(\mathbf{v}\)에 대하여 생각하면 첫 번째 계수 (♠︎)는 \(y\)를 상수로 생각한 상태에서 \(f(x,y)\)를 \(x\)로 미분한 것과 같다. 이 미분계수를 \(\left.\frac{\partial{f}}{\partial{x}}\right|_{\mathrm{P}}\)로 나타낸다. 같은 식으로, \(dx(\mathbf{v})=0\)인 경우를 생각하면 두 번째 계수 (♡)는 \(x\)를 상수로 생각한 상태에서 \(f(x,y)\)를 \(y\)로 미분한 것과 같고, 이 미분계수는 \(\left.\frac{\partial{f}}{\partial{y}}\right|_{\mathrm{P}}\)로 나타낸다. 이제 전체 결과를 정리하면
\[dz = \left.\frac{\partial{f}}{\partial{x}}\right|_{\mathrm{P}}\,dx + \left.\frac{\partial{f}}{\partial{y}}\right|_{\mathrm{P}}\,dy\]
가 된다.
이로써 우리는 변수가 몇 개이든 함수가 하나 주어지면 그 미분을 같은 방식으로 정의할 수 있다. 이런 게 바로 일반화의 위력이고 수학의 위력이라 하겠다.

 윤옥경_교수님을_추모하며.pdf
윤옥경_교수님을_추모하며.pdf