2009. 2. 14. 22:58
평균값 정리와 1/2 Math2009. 2. 14. 22:58
예전 홈페이지에 올렸던 글인데, 방명록에 요청하신 분이 있어 다시 올린다.
평균값 정리로부터 나오는 어떤 값의 극한값을 묻는 문제로, 정석에서는 특정한 함수를 주고 그 값을 묻는다. 어느 선생님은 "내가 해 본 웬만한 함수는 다 1/2이 나오더라"라고 하셨다는데, 그 이유까지는 알 수 없었다고 한다.
기본적으로 함수  가 Taylor series로 표현 가능하고
가 Taylor series로 표현 가능하고  \ne 0) 이면
이면  이 되는데, 이런 조건을 만족하지 않으면서도 1/2이 나오는 경우도 없지는 않겠지만 생각해 보지 않았다.
이 되는데, 이런 조건을 만족하지 않으면서도 1/2이 나오는 경우도 없지는 않겠지만 생각해 보지 않았다.
>  - f(a) = h f'(a%2b\theta h)) 인
인 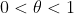 이 존재한다.
이 존재한다.
> 저 식에서 를 구해야하는 건데,
> 웬만한 함수들은 전부 1/2 이 나오네요.
> 왜 저 값이 1/2 이 나오는지, 혹 1/2 이 안 나오는 다른 함수가 있는지.
> 아시는 분은 좀 알려주셨으면 합니다.
함수 가 analytic, 즉 Taylor series로 표현 가능하면 항상 1/2이 나옵니다. 고등학교에서 배우는 함수는 거의 모두 analytic이니까 "웬만한 함수에 대해 1/2"인 게 당연하죠.
Taylor series를 이용하면,
다시 을 Taylor 전개하면,
첫번째 식에 대입하고, 로 바꾸면,
식을 정리하고, 양변을 으로 나눈 다음
하면,
따라서,
물론, 이란 조건은 주어져 있어야죠.
반응형
'Math' 카테고리의 다른 글
| Abel prize 2009 (7) | 2009.03.30 |
|---|---|
| 기하와 함수 (6) | 2009.03.19 |
| 소수와 솟수 (29) | 2009.02.11 |
| 선생님들, 이런 문제는 내지 마세요 3 (14) | 2009.02.08 |
| 음수 곱하기 음수는 양수 (12) | 2009.02.06 |


