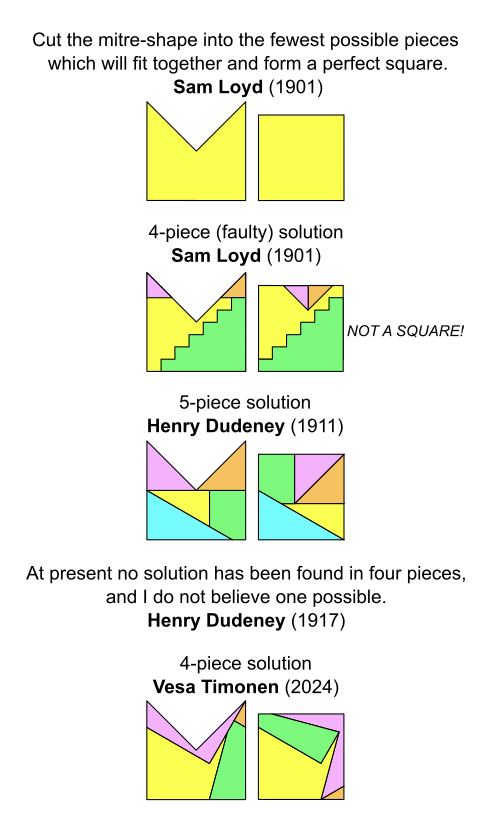
20세기 초 미국의 퍼즐 작가 샘 로이드는 삽화의 모양을 잘라 정사각형을 만드는 문제를 내었다. 저 모양은 정사각형을 대각선을 따라 사등분한 다음 한 조각을 떼어낸 것으로, 주교가 쓰는 관 모양을 닮아서 이 분할 퍼즐을 mitre puzzle이라 한다. 

로이드는 조각 개수가 가장 작은 분할을 찾아보라고 문제를 내었고, 조각 4개 짜리 답을 제시하였다. 진짜 절묘해 보이는 풀이인데…

사실 로이드의 답은 틀렸다. 오른쪽 모양이 정사각형에 가깝기는 하지만, 실제로는 가로 세로가 48:49인 직사각형이 되는 것을 간단한 계산으로 확인할 수 있다. 로이드 정도 되는 사람이 이걸 왜 몰랐을까? 

로이드와 쌍벽을 이루며 동시대에 활동했던 영국의 헨리 듀드니는 로이드의 오류를 지적하면서 조각 5개짜리 답을 제시하였다. (그림은 마지막에.)
수학퍼즐 분야에서 협력자이면서 경쟁자였던 두 사람의 관계를 보여주는 장면이랄까. 

나중에 미치 갤런트가 새로운 5조각 풀이를 발견했지만, 이후로 특별한 연구는 없었던 것 같다.  그러다 20세기말쯤 내가 새로운 5조각 풀이를 하나 더 찾았고, 몇년 전에 중국의 푸웨이가 참신한 5조각 풀이 하나와 6조각 풀이 몇개를 찾았다. 역시 그림은 마지막에.

2024년 1월쯤, 한국 최고의 퍼즐 작가라 할 만한 안진후님이 또다른 5조각 풀이를 발견하였다. 이로써 주교관 퍼즐의 5조각 풀이는 다섯 가지가 되었다. 아직 4조각 풀이는 발견되지 않았는데, 아마 불가능할 듯. 

혹시 새로운 분할 발견하신 분?

푸웨이 傅薇의 기존 풀이 해설과 관련 강연 영상. 
折纸思路新解百年数学题
2019年10月20日纪念马丁加德纳聚会活动下午场（二）

2024년 5월 드디어 4조각짜리 풀이가 유명한 퍼즐 작가 Vesa Timonen에 의해 발견되었다.

도형 분할 문제를 풀기 위한 프로그램을 작성하여 돌려본 결과, 한 조각을 뒤집어 사용하는 4조각짜리 풀이를 최초로 발견하였다.

자세한 정보는 https://mathstodon.xyz/@vesatimonen/112513347111148808 참고.

최근 한국산 콘텐츠들이 세계적인 인기를 끌고 있다. K-Pop과 K-Drama의 인기는 이미 세계적이며, 아카데미 영화제를 휩쓴 기생충도 유명하다. 얼마전에 넷플릭스(Netflix)에서 방송된 오징어 게임(Squid Game)은 전세계에서 그야말로 선풍적인 인기를 끌고 있다. 온갖 분야에서 한국인이 활약하는 모습을 보고 있으니 참 감격스럽다.

현재 세계에서 가장 유명한 퍼즐 작가라면 영국의 알렉스 벨로스(Alex Bellos)를 꼽을 수 있겠다. 다양한 퍼즐 책을 써서 세계적으로 인기를 끌었으며, 한국어로도 여러 권 번역이 되었다. 현재 영국의 신문 가디언(The Guardian)에 Alex Bellos's Monday puzzle을 격주로 연재하고 있다. 벨로스는 여러 퍼즐 작가들의 작품도 소개하고 있는데, 2021년 10월 4일 칼럼에서는 한국의 퍼즐 작가인 한동규 님의 걸작 분할 퍼즐을 소개하였다. 넷플릭스 오징어 게임의 스틸 한 장면과 함께.

사진도 그렇고, 제목도 "Can you solve it? Another game of brutal genius from South Korea"로 했으니, 최근의 한국 콘텐츠 인기를 의식하고 지은 게 분명한 제목이다.

세 종류의 분할 문제를 소개하고 있는데, 첫 번째 문제와 두 번째 문제는 크게 어렵지 않지만, 두 번째 문제를 참고로 하여 첫 번째 문제의 다른 풀이를 찾는 것은 조금 까다롭다. 가장 어려운 것은 체스의 킹(king)과 룩(Rook)을 맞바꾸는 세 번째 문제. 제목도 캐슬링(castling)이다. 벨로스가 "Marvel at its humour and elegance – and best of luck!"이라고 한 것처럼 정말 멋진 문제이다.

도전해 보기를!

\(ABCD = D \times \left( A^D + \dfrac{A}{D} - \dfrac{D}{A} \right) \)

12월 25일 뉴턴의 생일을 기념하여 복면산 문제 하나.

APPLE + APPLE + APPLE = NEWTON

뉴턴 시대에는 영국에서 그레고리력이 아닌 율리우스력을 쓰고 있었으므로, 그레고리력으로는 1642년 12월 25일이 아니라 1643년 1월 4일이 뉴턴의 생일이다. 

블로그 퍼즐 박물관(Puzzler Gang's Puzzle Museum)을 운영 중이신 퍼즐러갱 님께서 종이로 할 수 있는 퍼즐들을 모아 책을 내셨다. 알라딘 온라인 서점 주소는 여기.

뒤쪽에 스티커 형식으로 직접 만들어 볼 수 있는 자료(DIY 실물 퍼즐)까지 있어서 아주 좋다. 하루에 하나씩 해도 한 달 동안 아이들과 즐겁게 놀 수 있을 것 같다. 성질 급한 우리집 애들은 하루만에 다 뜯어서 만들어버릴 것 같지만.