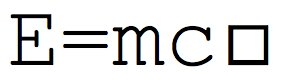유지원 박사님의 오리가미 물고기 이야기를 보고 떠오른 생각.

로버트 랭의 물고기 CP

저 물고기는 현존 최고의 origamist라 할 만한 Robert Lang(본업은 물리학자)의 작품으로, CP(crease pattern)로 보는 것과는 달리 단계가 꽤 많아서 깔끔하게 접기가 만만치 않다. 내가 좋아하는 물고기는 Davor Vinko의 작품으로 CP도 훨씬 간단하고, 아주 금방 접어낼 수 있다. 

Vinko의 물고기에서 인상적인 부분은 눈인데, 종이를 우그려 넣는 방식이 재미있다. Vinko는 이런 방식을 이전에 다른 작품에도 시도했는데, 물고기에서 아주 잘 구현되었다. Vinko는 이 방식을 이용하여 부엉이도 만들었다.

부엉이의 큰 눈에 아주 잘 어울리는 방식이다.

이 방식은 다른 origamist에게도 영감을 주어, Lang만큼이나 지존인 Joseph Wu 선생은 이런 작품을 만들어내었다.

 

더 발전하여 이런 것도.

Wu 선생은 CP도 공개하셨으나, 나는 CP만 보고도 접어내는 analyst 수준이 아니다 보니 구경만. -_- 아무튼 종이접기의 새로운 표현 방식이 다양한 작품으로 발전해 가는 것을 보니 정말 멋지다.

얼마 전에 인터넷에서 화제가 된 머그(mug)가 있었다. "I ♡ UNICODE"라는 문장에서 유니코드(unicode)로 표현된 하트 ♡가 깨져서 네모로 나타난 것이었다.

수학의 세계에는 별별 희한한 수열들이 많다. 피보나치 수열이나 메르센 수처럼 이름 붙은 유명한 수열도 있지만, 해괴한 규칙에 따라 만들어지는 수열도 있고, 뭔가 다른 계산을 하다가 나왔는데 아직 그 정체가 밝혀지지 않은 수열도 있다. 이런 수열들 가운데 비교적 수학적 의미가 있다고 인정되는 것들을 모아놓은 웹사이트가 있다. 수학자 슬론(Neil James Alexander Sloane)이 만든 On-Line Encyclopedia of Integer Sequences, 줄여서 OEIS가 그것으로, 처음에는 슬론이 종이에 적어 가며 수집한 목록 정도였지만, 지금은 독립된 도메인으로, 내용도 체계적으로 정리되어 있으며, 항목 수만 25만 개가 넘는다. 현재는 OEIS Foundation에서 관리하고 있다.

슬론은 OEIS에 있는 수열 가운데 가장 좋아하는 것으로 레카만 수열(Recamán sequence)을 들고 있다. OEIS 분류 번호 A005132인 이 수열은 콜롬비아의 수학자 베르나르도 레카만 산토스(Bernardo Recamán Santos)가 제안한 것으로, 규칙이 좀 희한하다. 먼저 \(a_0=0\)으로 둔다. 그 다음부터는 \(a_n = a_{n-1}-n\)으로 계산하되, 만약 이 값이 양수가 아니거나, 양수이더라도 이전 항에 이미 나온 수라면 \(a_n = a_{n-1}+n\)으로 바꾸어 계산한다.

몇 개 항을 계산해 보면, \(n=1\)일 때, \(a_0-1 = -1\)은 양수가 아니므로, \(a_1 = a_0+1 = 1\)이 된다. 이어서, \(n=2\)일 때, \(a_1-2=-1\)이므로 \(a_2 = a_1+2=3\)이 된다. 같은 식으로, \(a_3 = a_2+3=6\)이다. \(n=4\)일 때, \(a_3-4=2\)인데, 이전 단계에서 \(2\)가 나타나지 않았으므로, \(a_4 = 2\)가 된다. 그 다음 항은 \(n\)을 더하여 \(a_5=a_4+5=7\), \(a_6=a_5+6=13\), \(a_7=a_6+7=20\)이고, 여덟 번째 항은 \(n=8\)을 빼서 \(a_8=a_7-8=12\)가 된다. 이런 식으로 70항까지 계산한 결과는 다음과 같다.

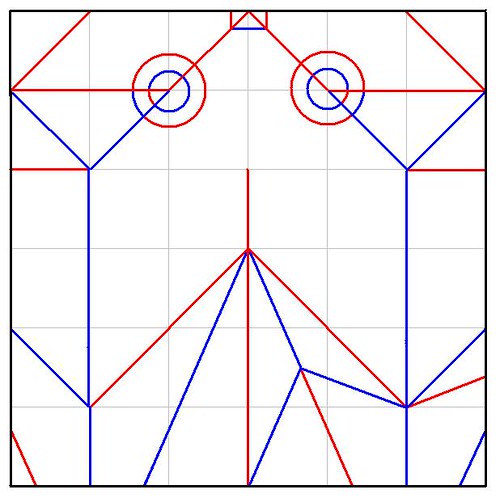
500항까지 구한 Recamán 수열

우선 생각해 볼 수 있는 질문이라면, 이 수열의 항이 모두 다를지 그렇지 않으면 같은 값이 나올 수 있을지일 것 같다. \(a_{n-1}-n\)이 이전 항에 나타나면 \(a_{n-1}+n\)을 계산하지만, \(a_{n-1}+n\)이 이전 항에 나타나는 경우에 대해서는 제한하지 않았기 때문이다. 이 질문은 간단히 답할 수 있다. 위에서 구한 항을 보면, \(a_{20}=a_{24}=42\)이므로 Recamán 수열에는 같은 값이 나올 수 있다. \(a_{18}=a_{26}=43\)도 위 표에서 찾을 수 있다.

이 수열에 중복되는 값이 나올 수는 있는 것은 쉽게 알 수 있겠는데, 이 수열이 모든 자연수를 만들어 낼 수는 있을까? 이 수열의 \(n\)번째 항은 앞 항과 \(n\) 차이가 나니까 그럴 것 같아 보이지는 않는다. 하지만 한편으로는 수열이 커졌다가 작아졌다가를 반복하는 형태여서 모든 자연수를 만들어 낼 수도 있을 것처럼 보인다. 어느 쪽이 참일까?

2001년에 AT&T의 앨런 윌크스(Allan Wilks)는 \(10^{15}\)번째 항까지 계산한 결과에 나타나지 않은 가장 작은 자연수가 \(852655 = 5 \times 31 \times 5501\)임을 발표하였다. 2010년에는 인텔의 컴퓨터 공학자인 벤자민 채핀(Benjamin Chaffin)이 \(10^{230}\)번째 항까지 계산해서, 여전히 \(852655\)가 나타나지 않음을 확인하였다. 과연 이 수는 Recamán 수열에 절대 나타나지 않는 수일까?